Tổng hợp đầy đủ kiến thức Toán lớp 5 trọng tâm: số thập phân, tỉ số phần trăm, hình học, toán chuyển động đều. Bao gồm công thức dễ nhớ và các dạng bài tập có lời giải chi tiết giúp học sinh nắm vững kiến thức và đạt điểm cao. Cùng BSUC tham khảo ngay dưới đây nhé!
Tổng quan chương trình Toán lớp 5
Chương trình Toán lớp 5 được thiết kế theo hướng tích hợp và phát triển năng lực, tập trung vào việc xây dựng tư duy logic và kỹ năng giải quyết vấn đề. Nội dung học tập được chia thành các chủ đề lớn, từ kiến thức cơ bản đến nâng cao, tạo điều kiện cho học sinh tiếp cận toán học một cách toàn diện và có hệ thống.
Các chủ đề trọng tâm trong chương trình:
Số tự nhiên và phép toán nâng cao:
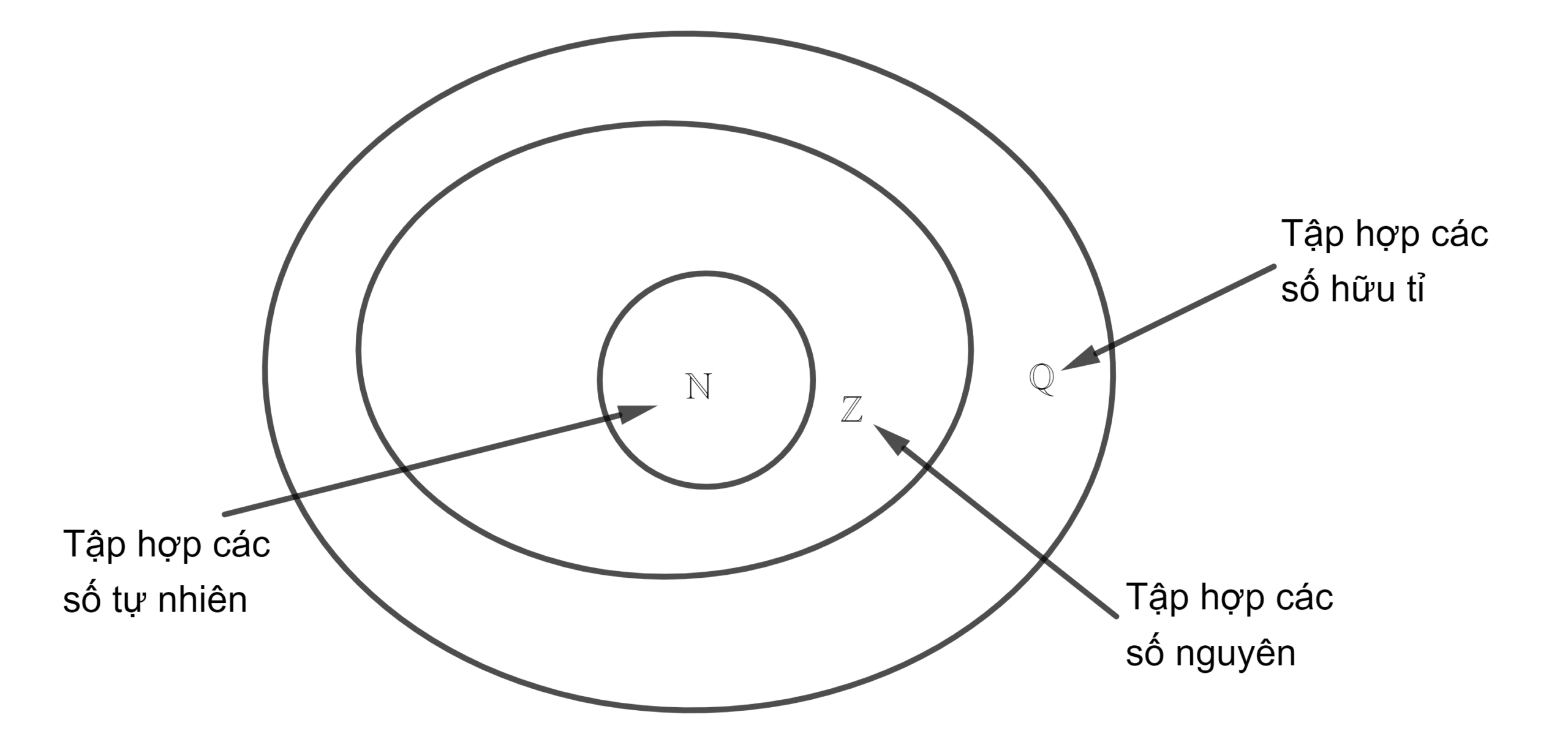
- Số tự nhiên đến hàng tỉ: đọc, viết, so sánh và sắp xếp
- Phép chia có dư và các tính chất của phép chia
- Ước số và bội số của một số tự nhiên
- Ước chung lớn nhất (ƯCLN) và bội chung nhỏ nhất (BCNN)
- Số nguyên tố và hợp số
Phân số và các phép toán:
- Khái niệm phân số, phân số bằng nhau
- Rút gọn phân số và quy đồng mẫu số
- Phép cộng, trừ, nhân, chia phân số
- So sánh phân số và sắp xếp phân số
- Hỗn số và chuyển đổi giữa hỗn số và phân số
Số thập phân và ứng dụng:
- Khái niệm số thập phân và cách đọc, viết
- Phép cộng, trừ, nhân, chia số thập phân
- Chuyển đổi giữa phân số và số thập phân
- Làm tròn số thập phân
- Ứng dụng số thập phân trong đời sống
Tỉ số phần trăm:
- Khái niệm tỉ số phần trăm
- Chuyển đổi giữa phân số, số thập phân và tỉ số phần trăm
- Bài toán về tỉ số phần trăm trong thực tế
- Tính lãi suất đơn giản
Hình học và đo lường:
- Diện tích các hình: tam giác, hình thang, hình bình hành
- Thể tích hình hộp chữ nhật và hình lập phương
- Đơn vị đo thể tích và chuyển đổi
- Biểu đồ và thống kê đơn giản

>>> THAM KHẢO: Công thức tính diện tích tam giác đầy đủ A-Z
Tài liệu ôn tập toàn diện với bài tập minh họa
I. SỐ HỌC
1. Các phép tính cơ bản
A) Số tự nhiên
Lý thuyết:
- Số tự nhiên là các số: 0, 1, 2, 3, 4, 5…
- Thứ tự thực hiện phép tính: () → × : → + –
Ví dụ minh họa:
Tính: 15 × 6 + 48 : 8 – 12
= 90 + 6 – 12
= 96 – 12
= 84
Bài tập:
- Tính: 125 × 8 + 375 : 25
- Tính hợp lý: 25 × 17 × 4
- Tính nhẩm: 99 × 11
Đáp án:
- 125 × 8 + 375 : 25 = 1000 + 15 = 1015
- 25 × 17 × 4 = 25 × 4 × 17 = 100 × 17 = 1700
- 99 × 11 = (100-1) × 11 = 1100 – 11 = 1089
B) Số thập phân
Lý thuyết:
- Cộng, trừ: Đặt tính thẳng cột, thẳng hàng dấu phẩy
- Nhân: Nhân như số tự nhiên, đếm chữ số thập phân
- Chia: Chia như số tự nhiên, chú ý đặt dấu phẩy
Ví dụ minh họa:
Tính: 12,5 × 2,4
= 125 × 24 ÷ 100 (vì có 2 chữ số thập phân)
= 3000 ÷ 100
= 30
Bài tập:
- 315,8 + 96,27
- 28,58 × 6,2
- 13,65 : 1,25
Đáp án:
- 315,8 + 96,27 = 412,07
- 28,58 × 6,2 = 177,196
- 13,65 : 1,25 = 10,92
C) Phân số
Lý thuyết:
- Quy đồng mẫu số rồi cộng, trừ tử số
- Nhân phân số: Nhân tử với tử, mẫu với mẫu
- Chia phân số: Nhân với phân số nghịch đảo
Ví dụ minh họa:
Tính: 2/3 + 3/4
= 8/12 + 9/12 = 17/12
Bài tập:
- 3/5 + 2/7
- 4/9 × 3/8
- 5/6 : 2/3
Đáp án:
- 3/5 + 2/7 = 21/35 + 10/35 = 31/35
- 4/9 × 3/8 = 12/72 = 1/6
- 5/6 : 2/3 = 5/6 × 3/2 = 15/12 = 5/4
2. Chuyển đổi phân số – số thập phân – phần trăm
Lý thuyết:
- Phân số → Số thập phân: Chia tử cho mẫu
- Số thập phân → Phần trăm: Nhân với 100, thêm dấu %
- Phần trăm → Phân số: Chia cho 100
Ví dụ minh họa:
0,725 = 725/1000 = 29/40 = 72,5%
Bài tập:
- Viết 3/8 dưới dạng số thập phân và phần trăm
- Viết 0,64 dưới dạng phân số tối giản
- 85% bằng phân số nào?
Đáp án:
- 3/8 = 0,375 = 37,5%
- 0,64 = 64/100 = 16/25
- 85% = 85/100 = 17/20
3. Tìm x (Giải phương trình đơn giản)
Lý thuyết:
- x + a = b → x = b – a
- x – a = b → x = b + a
- a × x = b → x = b : a
- x : a = b → x = b × a
Bài tập:
- x + 15,6 = 42,3
- x × 2,5 = 17,5
- x : 4 = 1,25
Đáp án:
- x = 42,3 – 15,6 = 26,7
- x = 17,5 : 2,5 = 7
- x = 1,25 × 4 = 5
>>> XEM THÊM: Công thức tính diện tích hình tròn – Mẹo ghi nhớ
II. DẠNG TOÁN VỀ QUAN HỆ SỐ
4. Tìm hai số khi biết tổng, hiệu, tỉ số
A) Biết tổng và hiệu
Công thức:
- Số lớn = (Tổng + Hiệu) : 2
- Số bé = (Tổng – Hiệu) : 2
Ví dụ: Tổng 100, hiệu 20
- Số lớn = (100 + 20) : 2 = 60
- Số bé = (100 – 20) : 2 = 40
Bài tập:
- Tổng hai số là 84, hiệu là 16. Tìm hai số.
- Hai số có tổng 156, số lớn hơn số bé 38. Tìm hai số.
Đáp án:
- Số lớn = (84 + 16) : 2 = 50; Số bé = (84 – 16) : 2 = 34
- Số lớn = (156 + 38) : 2 = 97; Số bé = (156 – 38) : 2 = 59
B) Biết tổng và tỉ số
Phương pháp: Chia tổng thành các phần theo tỉ số
Ví dụ: Tổng 120, tỉ số 2:3
- Tổng số phần: 2 + 3 = 5 phần
- Số thứ nhất: 120 × 2 : 5 = 48
- Số thứ hai: 120 × 3 : 5 = 72
Bài tập:
- Hai số có tổng 150, tỉ số 3:2. Tìm hai số.
- Ba số có tổng 180, tỉ số 2:3:4. Tìm ba số.
Đáp án:
- Số thứ nhất = 150 × 3 : 5 = 90; Số thứ hai = 150 × 2 : 5 = 60
- Số thứ nhất = 180 × 2 : 9 = 40; Số thứ hai = 60; Số thứ ba = 80
5. Toán về tỉ số, phần trăm
Lý thuyết:
- Tìm a% của số A: A × a : 100
- Tìm số khi biết a% của nó bằng B: B × 100 : a
Ví dụ: 15% của 320kg là: 320 × 15 : 100 = 48kg
Bài tập:
- 25% của 840 là bao nhiêu?
- Tìm số mà 30% của nó bằng 72.
- Một cửa hàng giảm giá 20%, khách hàng phải trả 160.000 đồng. Giá ban đầu là bao nhiêu?
Đáp án:
- 840 × 25 : 100 = 210
- 72 × 100 : 30 = 240
- 160.000 : 80 × 100 = 200.000 đồng
6. Toán trung bình cộng
Công thức: Trung bình cộng = Tổng : Số số hạng
Ví dụ: Trung bình cộng của 10, 20, 30 là (10+20+30):3 = 20
Bài tập:
- Trung bình cộng của 5 số là 16. Tổng của 5 số đó là bao nhiêu?
- An có điểm 4 bài kiểm tra: 8, 7, 9, 6. Bài thứ 5 phải được bao nhiêu điểm để trung bình cộng là 8?
Đáp án:
- Tổng = 16 × 5 = 80
- Tổng cần có = 8 × 5 = 40; Bài 5 = 40 – (8+7+9+6) = 10 điểm
III. ỨNG DỤNG THỰC TIỄN
7. Toán chuyển động đều
Công thức cơ bản:
- Quãng đường = Vận tốc × Thời gian (s = v × t)
- Vận tốc = Quãng đường : Thời gian (v = s : t)
- Thời gian = Quãng đường : Vận tốc (t = s : v)
Ví dụ: Xe đi 40km/h, đoạn đường 160km → Thời gian = 160 : 40 = 4 giờ
Dạng bài gặp nhau:
Hai xe ngược chiều: v_gặp = v₁ + v₂ Hai xe cùng chiều: v_đuổi = v₁ – v₂
Bài tập:
- Ô tô đi từ A đến B với vận tốc 60km/h trong 2,5 giờ. Quãng đường AB dài bao nhiêu?
- Hai xe khởi hành cùng lúc từ A và B cách nhau 180km, đi ngược chiều. Xe thứ nhất đi 45km/h, xe thứ hai đi 55km/h. Hỏi sau bao lâu hai xe gặp nhau?
- Một người đi bộ với vận tốc 5km/h. Sau đó 1 giờ, một người đi xe đạp với vận tốc 15km/h đuổi theo. Hỏi sau bao lâu kể từ khi xe đạp khởi hành thì hai người gặp nhau?
Đáp án:
- s = 60 × 2,5 = 150km
- t = 180 : (45 + 55) = 180 : 100 = 1,8 giờ = 1 giờ 48 phút
- Khi xe đạp khởi hành, người đi bộ đã đi được 5km. Thời gian gặp nhau: 5 : (15-5) = 0,5 giờ = 30 phút
8. Toán về đại lượng, tỉ lệ
A) Chuyển đổi đơn vị
Bảng đơn vị thường dùng:
- Độ dài: km → hm → dam → m → dm → cm → mm (×10)
- Diện tích: km² → ha → dam² → m² → dm² → cm² → mm² (×100)
- Thể tích: m³ → dm³ → cm³ → mm³ (×1000); 1dm³ = 1 lít
Bài tập:
- 2,5km² = ? ha = ? m²
- 3,2m³ = ? dm³ = ? lít
- 450cm = ? m = ? km
Đáp án:
- 2,5km² = 250 ha = 2.500.000 m²
- 3,2m³ = 3200 dm³ = 3200 lít
- 450cm = 4,5m = 0,0045km
B) Tỉ lệ thuận – nghịch
Tỉ lệ thuận: a₁/a₂ = b₁/b₂ Tỉ lệ nghịch: a₁ × b₁ = a₂ × b₂
Bài tập:
- 5 công nhân làm xong công việc trong 8 ngày. Hỏi 10 công nhân làm xong trong bao nhiêu ngày? (cùng năng suất)
- Một ô tô đi với vận tốc 60km/h hết 3 giờ. Nếu đi với vận tốc 45km/h thì hết bao nhiêu thời gian?
Đáp án:
- Tỉ lệ nghịch: 5 × 8 = 10 × x → x = 40 : 10 = 4 ngày
- Tỉ lệ nghịch: 60 × 3 = 45 × x → x = 180 : 45 = 4 giờ
IV. HÌNH HỌC
9. Chu vi và diện tích
A) Các công thức cơ bản
Hình vuông:
- Chu vi: P = 4 × a
- Diện tích: S = a²
Hình chữ nhật:
- Chu vi: P = (a + b) × 2
- Diện tích: S = a × b
Hình tam giác:
- Chu vi: P = a + b + c
- Diện tích: S = (a × h) : 2
Hình thang:
- Chu vi: P = a + b + c + d
- Diện tích: S = (a + b) × h : 2
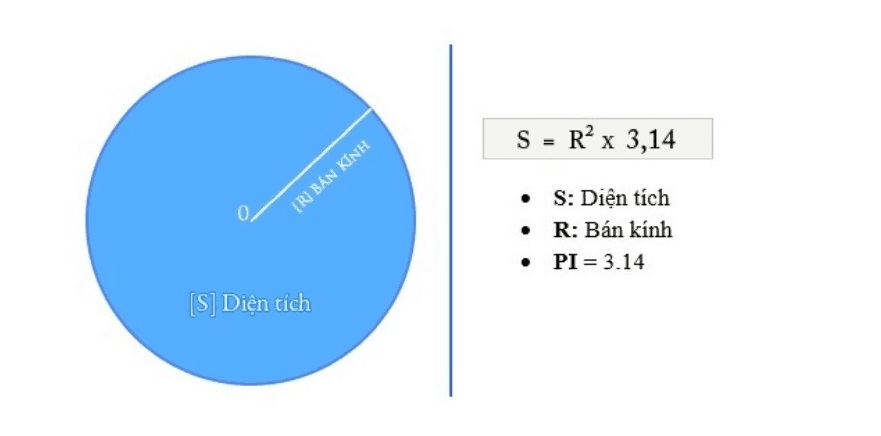
Hình tròn:
- Chu vi: P = d × 3,14 hoặc 2 × r × 3,14
- Diện tích: S = r × r × 3,14
Bài tập:
- Một mảnh đất hình chữ nhật có chu vi 180m, chiều rộng 40m. Tính diện tích mảnh đất.
- Một hình thang có đáy lớn 12m, đáy bé 8m, chiều cao 5m. Tính diện tích.
- Một bánh xe có bán kính 35cm. Bánh xe lăn được 10 vòng thì đi được quãng đường bao xa?
Đáp án:
- Chiều dài = 180 : 2 – 40 = 50m; S = 50 × 40 = 2000m²
- S = (12 + 8) × 5 : 2 = 50m²
- Chu vi bánh xe = 35 × 2 × 3,14 = 219,8cm; Quãng đường = 219,8 × 10 = 2198cm = 21,98m
10. Thể tích
Công thức:
Hình hộp chữ nhật: V = a × b × c Hình lập phương: V = a³
Bài tập:
- Một bể nước hình hộp chữ nhật có kích thước: dài 2m, rộng 1,5m, cao 1,2m. Tính thể tích bể nước.
- Một thùng hình lập phương có cạnh 80cm. Tính thể tích thùng theo dm³.
- Một phòng học dài 8m, rộng 6m, cao 3,5m. Tính thể tích không khí trong phòng.
Đáp án:
- V = 2 × 1,5 × 1,2 = 3,6m³
- 80cm = 8dm; V = 8³ = 512dm³
- V = 8 × 6 × 3,5 = 168m³
V. BÀI TOÁN CÓ LỜI VĂN
11. Phương pháp giải bài toán thực tế
Các bước giải:
- Đọc hiểu đề bài: Xác định dữ kiện và yêu cầu
- Phân tích: Tìm mối liên hệ giữa các dữ kiện
- Lập kế hoạch: Chọn phương pháp giải phù hợp
- Thực hiện: Tính toán theo kế hoạch
- Kiểm tra: Đối chiếu kết quả với thực tế
Ví dụ minh họa:
Đề bài: “Một cửa hàng nhập về 240kg táo. Ngày đầu bán được 2/5 số táo. Ngày thứ hai bán được 30% số táo còn lại. Hỏi sau 2 ngày còn lại bao nhiêu kg táo?”
Lời giải:
- Ngày đầu bán được: 240 × 2/5 = 96kg
- Sau ngày đầu còn: 240 – 96 = 144kg
- Ngày thứ hai bán được: 144 × 30% = 43,2kg
- Sau 2 ngày còn: 144 – 43,2 = 100,8kg
Bài tập thực hành:
- Toán về tiền: Mẹ đi chợ mang theo 200.000 đồng. Mẹ mua thịt hết 1/4 số tiền, mua rau hết 30% số tiền còn lại. Hỏi mẹ còn lại bao nhiêu tiền?
- Toán về năng suất: Một đội công nhân dự định làm đường trong 20 ngày, mỗi ngày làm 150m. Thực tế họ làm mỗi ngày 200m. Hỏi họ hoàn thành công việc sớm hơn dự định bao nhiêu ngày?
- Toán hỗn hợp: Trong bể có 1200 lít nước. Người ta mở vòi thứ nhất chảy vào bể 45 lít/phút, vòi thứ hai chảy ra 30 lít/phút. Nếu mở cả 2 vòi thì sau 40 phút bể có bao nhiêu lít nước?
Đáp án:
- Mua thịt: 200.000 × 1/4 = 50.000đ; Còn lại: 150.000đ; Mua rau: 150.000 × 30% = 45.000đ; Còn lại: 105.000đ
- Tổng công việc: 20 × 150 = 3000m; Thực tế cần: 3000 : 200 = 15 ngày; Sớm hơn: 20 – 15 = 5 ngày
- Mỗi phút tăng: 45 – 30 = 15 lít; Sau 40 phút tăng: 15 × 40 = 600 lít; Tổng: 1200 + 600 = 1800 lít
VI. DẠNG TOÁN NÂNG CAO
12. Toán logic và suy luận
A) Toán về tuổi:
Phương pháp: Hiệu số tuổi không đổi theo thời gian
Ví dụ: Ba hơn con 24 tuổi. Sau 6 năm nữa ba gấp 3 lần tuổi con. Tính tuổi hiện tại.
- Gọi tuổi con hiện tại là x
- Tuổi ba hiện tại: x + 24
- Sau 6 năm: Ba có (x + 24 + 6) tuổi, con có (x + 6) tuổi
- Theo đề: x + 30 = 3(x + 6)
- Giải: x + 30 = 3x + 18 → 2x = 12 → x = 6
- Vậy con 6 tuổi, ba 30 tuổi
Bài tập:
- Mẹ hơn con 28 tuổi. 4 năm trước đây mẹ gấp 5 lần tuổi con. Tính tuổi hiện tại của mỗi người.
- Tổng tuổi cha và con hiện nay là 50 tuổi. Biết 10 năm trước cha gấp 7 lần tuổi con. Tính tuổi mỗi người.
B) Toán về số:
Bài tập:
- Tìm số có 3 chữ số, biết rằng nếu viết thêm chữ số 4 vào bên trái số đó thì được số mới gấp 3 lần số ban đầu.
- Một số khi chia cho 15 dư 7, chia cho 25 dư 17. Tìm số đó biết số đó nhỏ hơn 300.
13. Toán hình học nâng cao
Bài tập:
- Một hình chữ nhật có chu vi 36cm. Nếu tăng chiều dài 4cm và giảm chiều rộng 2cm thì diện tích tăng 8cm². Tính kích thước ban đầu.
- Một thửa ruộng hình thang có diện tích 450m². Đáy bé 15m, chiều cao 18m. Tính đáy lớn.
PHẦN BÀI TẬP TỔNG HỢP
Đề kiểm tra mẫu:
Câu 1 (2 điểm): Thực hiện phép tính a) 3,25 + 16,8 × 2,5 b) 7/12 – 2/9 + 5/18
Câu 2 (2 điểm): Tìm x a) x × 2,4 = 19,2 b) x – 3/7 = 2/5
Câu 3 (2 điểm): Hai số có tổng là 156 và tỉ số 7:5. Tìm hai số đó.
Câu 4 (2 điểm): Một mảnh vườn hình thang có đáy lớn 45m, đáy bé bằng 2/3 đáy lớn, chiều cao 24m. Tính diện tích mảnh vườn.
Câu 5 (2 điểm): Một ô tô đi từ A đến B với vận tốc 50km/h hết 3,6 giờ. Lúc về, ô tô đi với vận tốc 60km/h. Tính thời gian lúc về.
Chúc các em học tốt và đạt kết quả cao! 🌟
Toán lớp 5 là bước đệm quan trọng trong hành trình học toán của học sinh, đòi hỏi sự chuẩn bị kỹ lưỡng và phương pháp học phù hợp. Với sự đa dạng về chương trình học, tài liệu hỗ trợ và phương pháp giảng dạy hiện đại, học sinh có nhiều cơ hội để thành công trong môn học này.
Bạn đang đọc bài viết Tổng hợp các dạng bài tập toán lớp 5 thường gặp tại chuyên mục Kỹ Năng và Kiến Thức cho bé trên website BSUC.