Q là tập hợp số gì? Tập hợp Q là một khái niệm quan trọng trong toán học, đặc biệt trong chương trình Toán lớp 7. Bài viết này, BSUC sẽ giúp bạn hiểu rõ về định nghĩa, ký hiệu và các tính chất của tập hợp số hữu tỉ Q một cách đầy đủ và dễ hiểu nhất.
Q là tập hợp số gì?
Tập hợp Q là tập hợp tất cả các số hữu tỉ. Đây là một tập hợp số quan trọng trong hệ thống số học, bao gồm tất cả các số có thể biểu diễn dưới dạng phân số.
Ký hiệu: Q (chữ Q viết hoa)
Nguồn gốc: Ký hiệu Q xuất phát từ tiếng Đức “Quotient” có nghĩa là “thương số”, phản ánh bản chất của số hữu tỉ là kết quả của phép chia.
Q gồm các loại số sau:
- Tất cả các số nguyên
- Số thập phân hữu hạn
- Số thập phân vô hạn tuần hoàn
- Các phân số có mẫu số khác 0
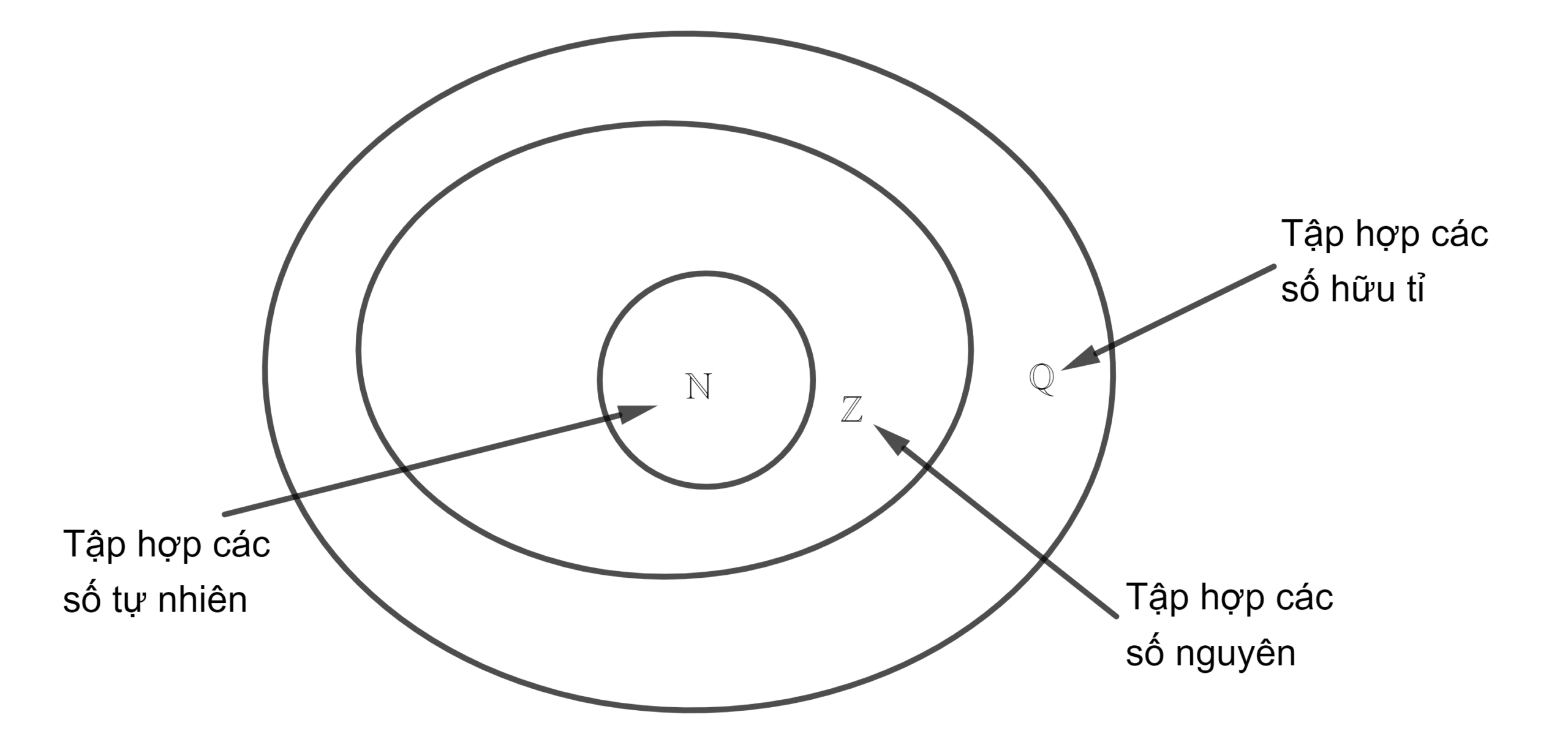
Định nghĩa tập hợp số hữu tỉ
Số hữu tỉ là số có thể viết dưới dạng phân số a/b trong đó:
- a ∈ Z (a là số nguyên)
- b ∈ Z (b là số nguyên)
- b ≠ 0 (mẫu số khác 0)
Ký hiệu toán học: Q = {a/b | a, b ∈ Z, b ≠ 0}
Nguồn gốc ký hiệu Q trong toán học
Ký hiệu Q được sử dụng từ thế kỷ 19, bắt nguồn từ từ tiếng Đức “Quotient” (thương số). Điều này phản ánh bản chất của số hữu tỉ là kết quả của phép chia giữa hai số nguyên.
Ký hiệu này được toán học quốc tế chấp nhận rộng rãi và sử dụng thống nhất trên toàn thế giới, giúp việc giao tiếp toán học trở nên dễ dàng hơn.
Các tính chất của tập hợp Q
Tập hợp Q có những tính chất toán học quan trọng sau:
- Tính đếm được: Q là tập hợp đếm được vô hạn
- Tính trù mật: Giữa hai số hữu tỉ bất kỳ luôn tồn tại vô số số hữu tỉ khác
- Có thứ tự: Các số hữu tỉ có thể so sánh và sắp xếp theo thứ tự tăng dần hoặc giảm dần
- Có số đối: Mọi số hữu tỉ đều có số đối thuộc Q
- Đóng với các phép toán: Kết quả của phép cộng, trừ, nhân, chia (khác 0) hai số hữu tỉ vẫn là số hữu tỉ
Q bao gồm các dạng số nào?
| Dạng số | Ví dụ | Cách viết dưới dạng a/b |
| Số nguyên | 5, -3, 0 | 5/1, -3/1, 0/1 |
| Phân số thường | 2/3, -5/7, 11/4 | Giữ nguyên |
| Số thập phân hữu hạn | 0.5, -2.75, 1.25 | 1/2, -11/4, 5/4 |
| Số thập phân vô hạn tuần hoàn | 0.333…, 1.666… | 1/3, 5/3 |
Ví dụ minh họa số hữu tỉ trong Q
Dưới đây là các ví dụ cụ thể về cách viết số dưới dạng hữu tỉ:
Số 3: Có thể viết thành 3/1, 6/2, 9/3, 12/4…
Số -0.25: Có thể viết thành -1/4, -2/8, -3/12…
Số 1.5: Có thể viết thành 3/2, 6/4, 9/6…
Số 0.666…: Có thể viết thành 2/3
Số -2.333…: Có thể viết thành -7/3
Phân biệt Q với các tập hợp số khác
Để hiểu rõ vị trí của Q trong hệ thống số, cần so sánh với các tập hợp số khác:
- N ⊂ Z ⊂ Q ⊂ R: Quan hệ bao hàm giữa các tập hợp số
- Q ∪ I = R: Hợp của số hữu tỉ và số vô tỉ tạo thành số thực
- Q ∩ I = ∅: Không có số nào vừa hữu tỉ vừa vô tỉ
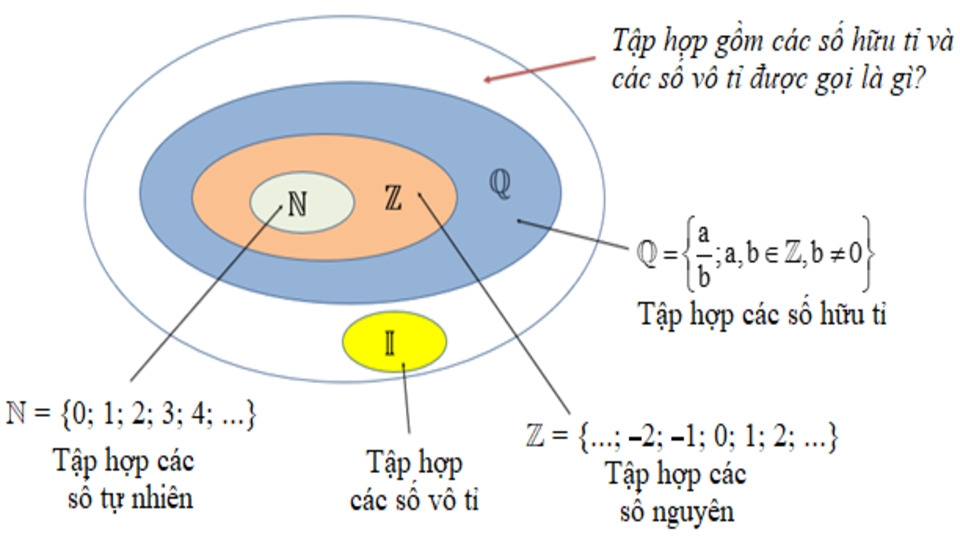
So sánh Q với Z, N, I, R
| Tập hợp | Ký hiệu | Đặc điểm | Ví dụ | Quan hệ với Q |
| Số tự nhiên | N | Số đếm từ 0 | 0, 1, 2, 3… | N ⊂ Q |
| Số nguyên | Z | Số âm, 0, số dương | …-2, -1, 0, 1, 2… | Z ⊂ Q |
| Số hữu tỉ | Q | Viết được dạng a/b | 1/2, -3/4, 2.5… | – |
| Số vô tỉ | I | Không viết được dạng a/b | √2, π, e… | Q ∩ I = ∅ |
| Số thực | R | Tất cả số trên trục số | Mọi số | Q ⊂ R |
Giải đáp thắc mắc về Q
1. Q là tập hợp số đếm được hay không?
Tập hợp Q là đếm được: Mặc dù vô hạn nhưng có thể liệt kê theo một trật tự nhất định • Điều này khác với tập hợp số thực R là không đếm được
2. Tập hợp nào lớn hơn Q?
Tập hợp số thực R chứa Q: R bao gồm cả số hữu tỉ và số vô tỉ • Tập hợp số phức C cũng chứa Q: C bao gồm số thực và số ảo
3. Tại sao 0.333… lại là số hữu tỉ?
Vì 0.333… = 1/3, có thể viết dưới dạng phân số với mẫu số khác 0.
4. Số π có thuộc Q không?
Không, π là số vô tỉ vì không thể viết dưới dạng a/b với a, b là số nguyên.
5. Mọi số thập phân đều là số hữu tỉ?
Không, chỉ có số thập phân hữu hạn và vô hạn tuần hoàn mới là số hữu tỉ.
Tóm lại, tập hợp Q là nền tảng quan trọng trong toán học, giúp chúng ta hiểu và áp dụng các khái niệm số học trong học tập và cuộc sống. Việc nắm vững định nghĩa, tính chất và cách nhận biết số hữu tỉ sẽ là bước đệm vững chắc cho các kiến thức toán học nâng cao sau này.
