Công thức tính diện tích tam giác là một trong những kiến thức toán học cơ bản và quan trọng nhất, được áp dụng rộng rãi từ chương trình học phổ thông đến các ứng dụng thực tế trong cuộc sống. Việc nắm vững các công thức tính diện tích tam giác không chỉ giúp học sinh giải quyết tốt các bài tập toán học.
>>> XEM THÊM: Tổng hợp các dạng bài tập toán lớp 5 thường gặp
Công thức tính diện tích tam giác thường
Công thức tính diện tích tam giác thường là nền tảng cho tất cả các loại tam giác khác. Công thức cơ bản được biểu diễn như sau:
S = (a × h) / 2
Trong đó:
- S: Diện tích tam giác (đơn vị: cm², m², dm²…)
- a: Độ dài cạnh đáy của tam giác
- h: Chiều cao tương ứng với cạnh đáy (đoạn thẳng vuông góc từ đỉnh đối diện xuống cạnh đáy)
Công thức này có nguồn gốc từ việc coi tam giác như một nửa hình bình hành. Khi vẽ một hình bình hành có cùng đáy và chiều cao với tam giác, diện tích tam giác sẽ bằng một nửa diện tích hình bình hành đó.
Bảng tóm tắt các thành phần:
| Thành phần | Ký hiệu | Mô tả | Lưu ý |
| Diện tích | S | Kết quả cần tìm | Luôn là số dương |
| Cạnh đáy | a | Một cạnh bất kỳ của tam giác | Có thể chọn cạnh nào thuận tiện nhất |
| Chiều cao | h | Khoảng cách vuông góc từ đỉnh đến đáy | Phải vuông góc với cạnh đáy |
Điều kiện áp dụng:
- Biết độ dài một cạnh và chiều cao tương ứng
- Có thể đo hoặc tính được chiều cao
- Tam giác phải hợp lệ (tổng hai cạnh bất kỳ lớn hơn cạnh thứ ba)
Ví dụ tính diện tích tam giác thường
Ví dụ 1: Tam giác cơ bản
- Cho tam giác ABC có cạnh đáy BC = 8 cm và chiều cao từ A xuống BC là 6 cm
- Áp dụng công thức: S = (8 × 6) / 2 = 24 cm²
Ví dụ 2: Bài toán thực tế
- Một mảnh đất hình tam giác có độ dài đáy 25 mét và chiều cao 18 mét
- Diện tích mảnh đất: S = (25 × 18) / 2 = 225 m²
Ví dụ 3: Tam giác với đơn vị khác nhau
- Cạnh đáy: 1.5 m = 150 cm
- Chiều cao: 80 cm
- Diện tích: S = (150 × 80) / 2 = 6000 cm² = 0.6 m²
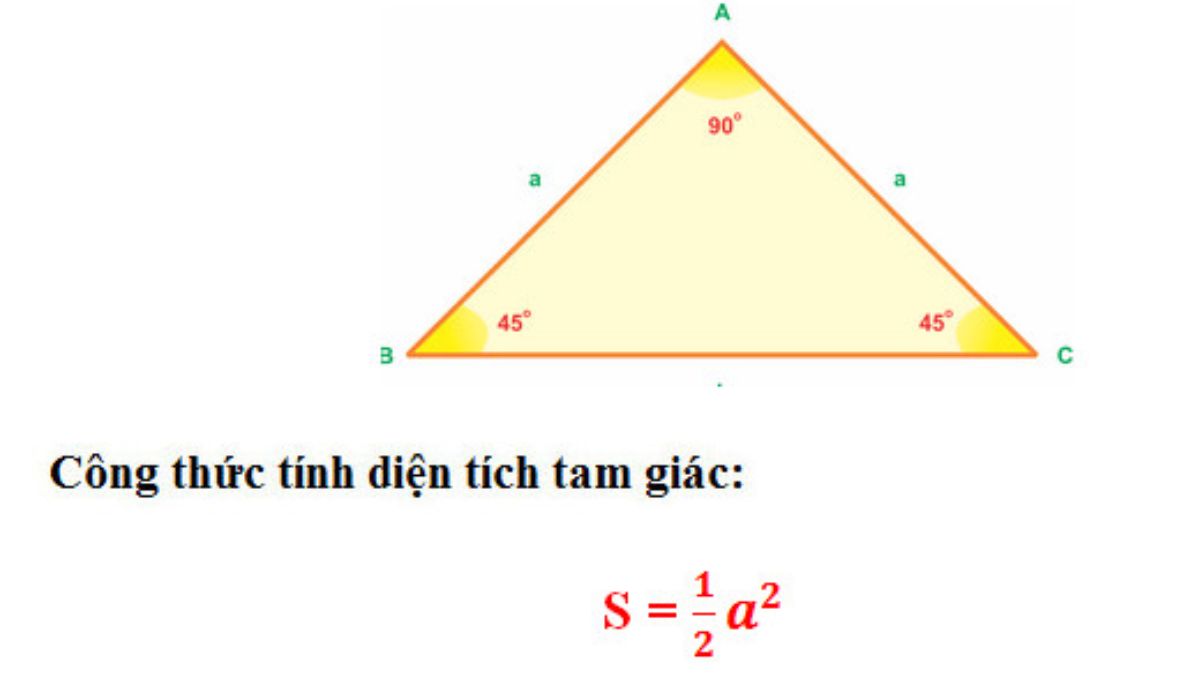
Công thức tính diện tích tam giác vuông
Tam giác vuông là loại tam giác đặc biệt có một góc bằng 90°. Điều này tạo ra sự thuận lợi lớn trong việc tính diện tích vì hai cạnh góc vuông có thể đóng vai trò là cạnh đáy và chiều cao.
Công thức cơ bản: S = (1/2) × a × b
Trong đó:
- a và b là độ dài hai cạnh góc vuông
- Không cần tính chiều cao riêng vì hai cạnh góc vuông vuông góc với nhau
Bảng so sánh với tam giác thường:
| Đặc điểm | Tam giác thường | Tam giác vuông |
| Công thức | S = (a × h)/2 | S = (a × b)/2 |
| Yêu cầu | Cạnh đáy + chiều cao | Hai cạnh góc vuông |
| Độ phức tạp | Trung bình | Đơn giản |
| Tần suất sử dụng | Cao | Rất cao |
Ví dụ minh họa:
Ví dụ 1: Tam giác vuông có hai cạnh góc vuông là 3 cm và 4 cm
- Diện tích: S = (3 × 4) / 2 = 6 cm²
Ví dụ 2: Mảnh đất hình tam giác vuông với hai cạnh góc vuông 15 m và 20 m
- Diện tích: S = (15 × 20) / 2 = 150 m²
>>> XEM THÊM: Công thức tính diện tích hình tròn – Mẹo ghi nhớ
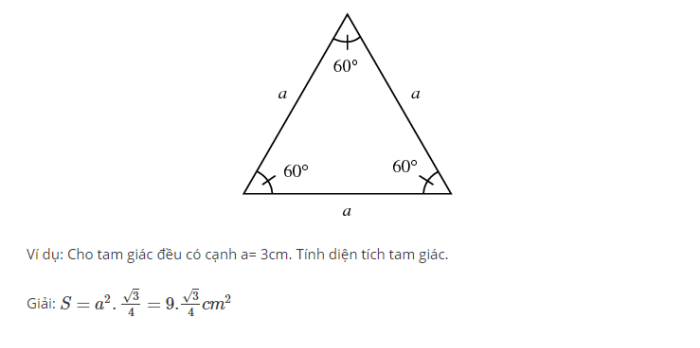
Công thức tính diện tích tam giác đều
Tam giác đều là tam giác có ba cạnh bằng nhau và ba góc bằng nhau (mỗi góc 60°). Đối với tam giác đều, chúng ta có hai công thức chính để tính diện tích.
Công thức 1: Sử dụng cạnh và chiều cao S = (a × h) / 2
Công thức 2: Chỉ cần biết độ dài cạnh S = (a² × √3) / 4
Trong đó:
- a: Độ dài cạnh của tam giác đều
- h: Chiều cao của tam giác đều
- √3 ≈ 1.732
Nguồn gốc công thức đặc biệt: Công thức S = (a² × √3) / 4 được suy ra từ việc tính chiều cao của tam giác đều. Trong tam giác đều có cạnh a, chiều cao h = (a × √3) / 2. Thay vào công thức cơ bản:
S = (a × h) / 2 = (a × (a × √3) / 2) / 2 = (a² × √3) / 4
Bảng tính nhanh cho các giá trị thông dụng:
| Cạnh (a) | Chiều cao (h) | Diện tích (S) | Ghi chú |
| 2 | 1.732 | 1.732 | √3 |
| 4 | 3.464 | 6.928 | 4√3 |
| 6 | 5.196 | 15.588 | 9√3 |
| 8 | 6.928 | 27.712 | 16√3 |
| 10 | 8.660 | 43.301 | 25√3 |
Ví dụ minh họa:
Ví dụ 1: Tam giác đều có cạnh 6 cm
- Cách 1: Tính chiều cao h = (6 × √3) / 2 = 3√3 ≈ 5.196 cm Diện tích: S = (6 × 5.196) / 2 ≈ 15.588 cm²
- Cách 2: S = (6² × √3) / 4 = (36 × √3) / 4 = 9√3 ≈ 15.588 cm²
Ví dụ 2: Tấm kim loại hình tam giác đều cạnh 8 cm
- Diện tích: S = (8² × √3) / 4 = (64 × √3) / 4 = 16√3 ≈ 27.712 cm²
Công thức Heron cho tam giác biết ba cạnh
Công thức Heron là một trong những công thức quan trọng nhất trong hình học, cho phép tính diện tích tam giác khi chỉ biết độ dài ba cạnh mà không cần biết chiều cao hay góc.
Công thức Heron: S = √[p(p-a)(p-b)(p-c)]
Trong đó:
- a, b, c: Độ dài ba cạnh của tam giác
- p: Nửa chu vi tam giác, p = (a + b + c) / 2
- S: Diện tích tam giác
Các bước áp dụng công thức Heron:
Bước 1: Kiểm tra tính hợp lệ của tam giác
Điều kiện: a + b > c, b + c > a, a + c > b
Bước 2: Tính nửa chu vi
p = (a + b + c) / 2
Bước 3: Tính các hiệu số
(p – a), (p – b), (p – c)
Bước 4: Áp dụng công thức
S = √[p × (p-a) × (p-b) × (p-c)]
Ví dụ chi tiết:
Ví dụ: Tam giác có ba cạnh a = 5, b = 12, c = 13
- Kiểm tra: 5 + 12 = 17 > 13 ✓, 12 + 13 = 25 > 5 ✓, 5 + 13 = 18 > 12 ✓
- Nửa chu vi: p = (5 + 12 + 13) / 2 = 15
- Các hiệu số: p – a = 15 – 5 = 10, p – b = 15 – 12 = 3, p – c = 15 – 13 = 2
- Diện tích: S = √[15 × 10 × 3 × 2] = √900 = 30
Ví dụ ứng dụng thực tế: Một mảnh đất có hình tam giác với ba cạnh hàng rào dài 120m, 150m và 180m. Cần tính diện tích để ước tính chi phí san lấp mặt bằng.
- p = (120 + 150 + 180) / 2 = 225
- S = √[225 × (225-120) × (225-150) × (225-180)]
- S = √[225 × 105 × 75 × 45] = √[80,156,250] ≈ 8,953 m²
Tổng hợp bài tập thực hành diện tích hình tam giác lớp 5
Bài tập cơ bản
Dạng 1: Tính diện tích khi biết đáy và chiều cao
Bài 1: Tam giác có đáy 8 cm, chiều cao 6 cm. Tính diện tích.
Lời giải: S = (8 × 6)/2 = 24 cm²
Bài 2: Tam giác có đáy 12 dm, chiều cao 9 dm. Tính diện tích.
Lời giải: S = (12 × 9)/2 = 54 dm²
Bài 3: Tam giác có đáy 15 m, chiều cao 8 m. Tính diện tích.
Lời giải: S = (15 × 8)/2 = 60 m²
Dạng 2: Tìm chiều cao hoặc đáy khi biết diện tích
Bài 4: Tam giác có diện tích 36 cm², đáy 9 cm. Tìm chiều cao.
Lời giải: h = (2 × 36)/9 = 8 cm
Bài 5: Tam giác có diện tích 45 dm², chiều cao 10 dm. Tìm đáy.
Lời giải: a = (2 × 45)/10 = 9 dm
Dạng 3: Bài toán thực tế
Bài 6: Một mảnh vườn hình tam giác có đáy 20 m, chiều cao 15 m. Hỏi diện tích mảnh vườn là bao nhiêu?
Lời giải: S = (20 × 15)/2 = 150 m²
Bài 7: Một cái ao hình tam giác có đáy 30 m, chiều cao 24 m. Tính diện tích mặt nước của ao.
Lời giải: S = (30 × 24)/2 = 360 m²
Bài tập nâng cao
Dạng 4: Tam giác vuông
Bài 8: Tam giác vuông có hai cạnh góc vuông lần lượt là 5 cm và 12 cm. Tính diện tích.
Lời giải: S = (5 × 12)/2 = 30 cm²
Bài 9: Tam giác vuông cân có cạnh góc vuông 8 cm. Tính diện tích.
Lời giải: S = (8 × 8)/2 = 32 cm²
Dạng 5: Tam giác đều
Bài 10: Tam giác đều có cạnh 6 cm. Tính diện tích.
Lời giải: S = (6² × √3)/4 = (36 × 1.732)/4 ≈ 15.59 cm²
Dạng 6: Công thức Heron
Bài 11: Tam giác có ba cạnh 6 cm, 8 cm, 10 cm. Tính diện tích.
Lời giải:
- p = (6 + 8 + 10)/2 = 12
- S = √[12 × (12-6) × (12-8) × (12-10)] = √[12 × 6 × 4 × 2] = √576 = 24 cm²
Bài tập tổng hợp
Bài 12: Bài toán phức hợp Một mảnh đất hình chữ nhật có chiều dài 40 m, chiều rộng 30 m. Người ta chia mảnh đất này thành hai phần bằng nhau bằng một đường chéo. Tính diện tích mỗi phần.
Lời giải:
- Diện tích hình chữ nhật: 40 × 30 = 1200 m²
- Mỗi tam giác có diện tích: 1200/2 = 600 m²
- Kiểm tra: S = (40 × 30)/2 = 600 m² ✓
Bài 13: Bài toán kinh tế Một thửa đất hình tam giác có đáy 25 m, chiều cao 20 m. Giá đất là 8 triệu đồng/m². Tính giá trị của thửa đất.
Lời giải:
- Diện tích: S = (25 × 20)/2 = 250 m²
- Giá trị: 250 × 8,000,000 = 2,000,000,000 đồng = 2 tỷ đồng
Bài 14: Bài toán tối ưu Từ một tấm cardboard hình vuông cạnh 12 cm, cắt ra tam giác đều có diện tích lớn nhất. Tính diện tích tam giác đó.
Lời giải:
- Tam giác đều lớn nhất nội tiếp hình vuông có cạnh = cạnh hình vuông = 12 cm
- Diện tích: S = (12² × √3)/4 = (144 × √3)/4 = 36√3 ≈ 62.35 cm²
Bài viết này đã trình bày đầy đủ các công thức tính diện tích tam giác từ cơ bản đến nâng cao, kèm theo ví dụ thực tế và ứng dụng trong nhiều lĩnh vực. BSUC hy vọng sẽ là tài liệu hữu ích cho việc học tập và ứng dụng của bạn đọc.
