Diện tích hình tròn là một trong những khái niệm toán học cơ bản và quan trọng nhất, được ứng dụng rộng rãi trong học tập từ tiểu học đến trung học cơ sở, cũng như trong thực tế cuộc sống. Bài viết này BSUC sẽ hướng dẫn chi tiết các công thức tính diện tích hình tròn, kèm theo ví dụ minh họa dễ hiểu và bài tập thực hành có đáp án.
>>> XEM THÊM: Tổng hợp các dạng bài tập toán lớp 5 thường gặp
| Cho biết | Công thức | Ký hiệu | Ví dụ |
| Bán kính r | S = πr² | π ≈ 3.14 hoặc 22/7 | r = 5cm → S = 3.14 × 5² = 78.5cm² |
| Đường kính d | S = π(d/2)² hoặc S = πd²/4 | d = 2r | d = 10cm → S = 3.14 × 5² = 78.5cm² |
| Chu vi C | S = C²/(4π) | C = 2πr | C = 31.4cm → S = 31.4²/(4×3.14) = 78.5cm² |
Công thức tính diện tích hình tròn theo bán kính
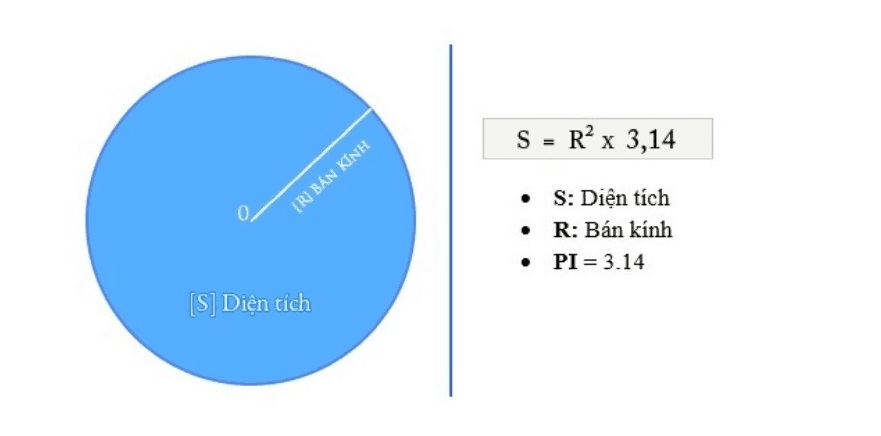
S = πr²
Đây là công thức cơ bản nhất và được sử dụng phổ biến nhất, trong đó:
- S: Diện tích hình tròn (đơn vị: cm², m², dm²…)
- π (Pi): Hằng số toán học ≈ 3.14159… (thường lấy 3.14 hoặc 22/7)
- r: Bán kính hình tròn (khoảng cách từ tâm đến mọi điểm trên đường tròn)
Ví dụ minh họa: Một hình tròn có bán kính 7cm. Tính diện tích?
- Giải: S = πr² = 3.14 × 7² = 3.14 × 49 = 153.86cm²
- Hoặc: S = 22/7 × 7² = 22/7 × 49 = 154cm²
Khi biết đường kính (d):
Vì đường kính d = 2r nên r = d/2, ta có:
- S = π(d/2)² = πd²/4
Ví dụ: Đường kính hình tròn là 14cm
- S = 3.14 × 14²/4 = 3.14 × 196/4 = 3.14 × 49 = 153.86cm²
Khi biết chu vi (C):
Từ công thức chu vi C = 2πr, suy ra r = C/(2π), thay vào công thức diện tích:
- S = π[C/(2π)]² = C²/(4π)
Ví dụ: Chu vi hình tròn là 44cm
- S = 44²/(4 × 3.14) = 1936/12.56 = 154.14cm²
Lưu ý quan trọng:
- Luôn đổi các đại lượng về cùng đơn vị trước khi tính
- Kết quả diện tích luôn có đơn vị bình phương (cm², m²…)
- Khi tính toán thực tế, chú ý làm tròn số hợp lý
Công thức tính diện tích nửa hình tròn & hình quạt tròn
Diện tích nửa hình tròn:
S = (πr²)/2
Đơn giản là lấy diện tích hình tròn chia đôi.
Ví dụ: Bán kính 6cm
- S = (3.14 × 6²)/2 = (3.14 × 36)/2 = 113.04/2 = 56.52cm²
Diện tích hình quạt tròn:
S = (πr²n)/360
Trong đó n là số đo cung (tính bằng độ).
Ví dụ: Hình quạt tròn bán kính 10cm, góc ở tâm 60°
- S = (3.14 × 10² × 60)/360 = (3.14 × 100 × 60)/360 = 52.33cm²
Ứng dụng thực tế:
- Tính diện tích cánh quạt, miếng bánh pizza hình quạt
- Xác định diện tích vùng tưới của vòi phun nước
- Tính diện tích vùng chiếu sáng của đèn pha
Các dạng bài tập tính diện tích hình tròn phổ biến
Dạng 1: Cho bán kính, tính diện tích
- Bài: Hình tròn có bán kính 4.5cm. Tính diện tích?
- Giải: S = 3.14 × 4.5² = 3.14 × 20.25 = 63.585cm²
Dạng 2: Cho đường kính, tính diện tích
- Bài: Đường kính 20cm. Tính diện tích?
- Giải: r = 20/2 = 10cm → S = 3.14 × 10² = 314cm²
Dạng 3: Cho chu vi, tính diện tích
- Bài: Chu vi 62.8cm. Tính diện tích?
- Giải: S = 62.8²/(4 × 3.14) = 3943.84/12.56 = 314cm²
Dạng 4: Bài toán thực tế
- Bài: Một bể nước hình tròn có đường kính 2m. Tính diện tích đáy bể?
- Giải: r = 2/2 = 1m → S = 3.14 × 1² = 3.14m²
Lưu ý khi làm bài:
- Đọc kỹ đề để phân biệt đường kính và bán kính
- Chú ý đơn vị trong đề bài và yêu cầu
- Với bài toán thực tế, vẽ hình minh họa sẽ dễ hình dung hơn
Các lỗi sai phổ biến khi tính diện tích hình tròn
- Nhầm lẫn giữa bán kính và đường kính
- Lỗi: Đề cho đường kính 10cm nhưng tính S = 3.14 × 10² = 314cm²
- Đúng: r = 10/2 = 5cm → S = 3.14 × 5² = 78.5cm²
- Quên đổi đơn vị
- Lỗi: Bán kính 5dm, đường kính 80cm → S = 3.14 × 5²?
- Đúng: Đổi 80cm = 8dm, r = 4dm → S = 3.14 × 4² = 50.24dm²
- Sử dụng giá trị π không chính xác
- Khi đề yêu cầu lấy π = 3.14 thì dùng 3.14
- Khi đề yêu cầu lấy π = 22/7 thì dùng 22/7
- Không tự ý thay đổi giá trị π
- Quên bình phương bán kính
- Lỗi: S = π × r thay vì S = π × r²
Mẹo kiểm tra: Nếu bán kính tăng gấp đôi, diện tích phải tăng gấp 4 lần (vì 2² = 4)
Hướng dẫn nhập máy tính:
- Bấm: 3.14 × (bán kính) × (bán kính) =
- Hoặc: 3.14 × (bán kính) x² =
Một số mẹo giúp tính nhanh công thức diện tích hình tròn
Câu 1: Khi chỉ biết chu vi, tính diện tích như thế nào?
- Từ chu vi C = 2πr, tìm bán kính: r = C/(2π)
- Sau đó áp dụng S = πr²
- Hoặc dùng trực tiếp: S = C²/(4π)
Câu 2: Công thức tính nửa hình tròn có gì khác?
- Diện tích nửa hình tròn = (Diện tích hình tròn)/2
- S = (πr²)/2
Câu 3: Nên lấy π bằng bao nhiêu?
- Trong bài tập: làm theo yêu cầu đề bài
- Tính toán thông thường: 3.14
- Tính chính xác hơn: 3.14159 hoặc dùng phím π trên máy tính
Câu 4: So sánh diện tích hình tròn với hình vuông cùng chu vi?
- Hình tròn luôn có diện tích lớn hơn
- Ví dụ: Cùng chu vi 12cm
- Hình vuông: cạnh 3cm → S = 9cm²
- Hình tròn: r ≈ 1.91cm → S ≈ 11.46cm²
Câu 5: Tại sao công thức lại là πr² chứ không phải công thức khác?
- Đây là kết quả chứng minh toán học từ thời cổ đại
- Pi (π) là tỷ lệ giữa chu vi và đường kính của mọi hình tròn
- Công thức được chứng minh qua phương pháp phân chia hình tròn thành các hình nhỏ
Việc nắm vững công thức tính diện tích hình tròn không chỉ giúp học sinh giải tốt bài tập trong SGK mà còn ứng dụng hiệu quả trong thực tế. Hãy luyện tập thường xuyên với các dạng bài đa dạng để thành thạo kỹ năng này!
